Pentagonal cupola
| Pentagonal cupola | |
|---|---|
 | |
| Type | Johnson J4 – J5 – J6 |
| Faces | 5 triangles 5 squares 1 pentagon 1 decagon |
| Edges | 25 |
| Vertices | 15 |
| Vertex configuration | |
| Symmetry group | |
| Properties | convex, elementary |
| Net | |
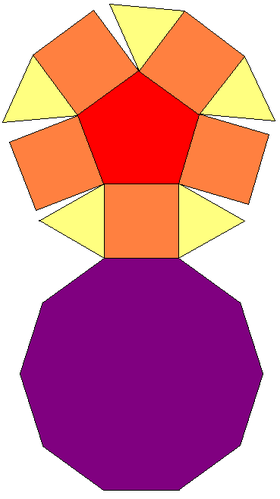 | |
In geometry, the pentagonal cupola is one of the Johnson solids (J5). It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon.
Properties
[edit]The pentagonal cupola's faces are five equilateral triangles, five squares, one regular pentagon, and one regular decagon.[1] It has the property of convexity and regular polygonal faces, from which it is classified as the fifth Johnson solid.[2] This cupola produces two or more regular polyhedrons by slicing it with a plane, an elementary polyhedron's example.[3]
The following formulae for circumradius , and height , surface area , and volume may be applied if all faces are regular with edge length :[4]
It has an axis of symmetry passing through the center of both top and base, which is symmetrical by rotating around it at one-, two-, three-, and four-fifth of a full-turn angle. It is also mirror-symmetric relative to any perpendicular plane passing through a bisector of the hexagonal base. Therefore, it has pyramidal symmetry, the cyclic group of order ten.[3]
Related polyhedron
[edit]The pentagonal cupola can be applied to construct a polyhedron. A construction that involves the attachment of its base to another polyhedron is known as augmentation; attaching it to prisms or antiprisms is known as elongation or gyroelongation.[5][6] Some of the Johnson solids with such constructions are: elongated pentagonal cupola , gyroelongated pentagonal cupola , pentagonal orthobicupola , pentagonal gyrobicupola , pentagonal orthocupolarotunda , pentagonal gyrocupolarotunda , elongated pentagonal orthobicupola , elongated pentagonal gyrobicupola , elongated pentagonal orthocupolarotunda , gyroelongated pentagonal bicupola , gyroelongated pentagonal cupolarotunda , augmented truncated dodecahedron , parabiaugmented truncated dodecahedron , metabiaugmented truncated dodecahedron , triaugmented truncated dodecahedron , gyrate rhombicosidodecahedron , parabigyrate rhombicosidodecahedron , metabigyrate rhombicosidodecahedron , and trigyrate rhombicosidodecahedron . Relatedly, a construction from polyhedra by removing one or more pentagonal cupolas is known as diminishment: diminished rhombicosidodecahedron , paragyrate diminished rhombicosidodecahedron , metagyrate diminished rhombicosidodecahedron , bigyrate diminished rhombicosidodecahedron , parabidiminished rhombicosidodecahedron , metabidiminished rhombicosidodecahedron , gyrate bidiminished rhombicosidodecahedron , and tridiminished rhombicosidodecahedron .[1]
References
[edit]- ^ a b Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. p. 62. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
- ^ a b Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
- ^ Braileanu1, Patricia I.; Cananaul, Sorin; Pasci, Nicoleta E. (2022). "Geometric pattern infill influence on pentagonal cupola mechanical behavior subject to static external loads". Journal of Research and Innovation for Sustainable Society. 4 (2). Thoth Publishing House: 5–15. doi:10.33727/JRISS.2022.2.1:5-15 (inactive 16 December 2024). ISSN 2668-0416.
{{cite journal}}: CS1 maint: DOI inactive as of December 2024 (link) CS1 maint: numeric names: authors list (link) - ^ Demey, Lorenz; Smessaert, Hans (2017). "Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation". Symmetry. 9 (10): 204. Bibcode:2017Symm....9..204D. doi:10.3390/sym9100204.
- ^ Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms" (PDF). Journal for Geometry and Graphics. 19 (1): 79–91.





































